发表于 | 分类于 | 0 | 阅读次数 668

目录导航

# 介绍 堆排序（英语：Heapsort，wiki百科）是指利用堆这种数据结构所设计的一种排序算法。

堆是一个近似完全二叉树的结构，并同时满足堆积的性质：即子节点的键值或索引总是小于（或者大于）它的父节点。

堆排序是一种选择排序，它的最坏，最好，平均时间复杂度均为O(nlogn)，它也是不稳定排序。

关于堆（Heap）

堆是一颗完全二叉树，且除了完全二叉树以外还具有以下特征：每个节点的值都大于或等于其左右孩子结点的值，称为大堆顶；或者每个结点的值都小于或等于其左右孩子的值，称为小堆顶。

如图：

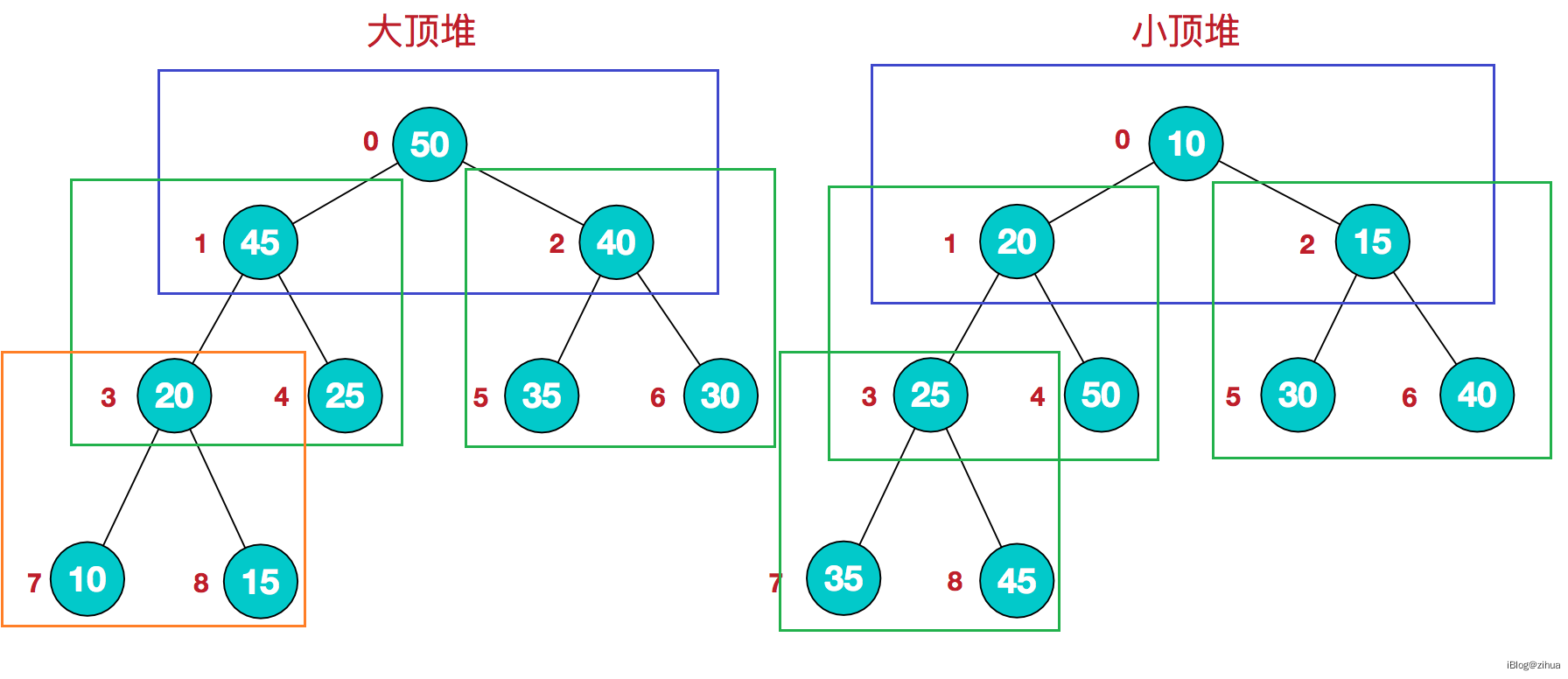
image.png

大堆顶中，我框选出来的三个元素，永远都是根最大；小堆顶中框选出来的三个元素，永远都是根最小。满足任意框选一个根和其左右结点的树满足这个条件，就被称为堆。

由于堆的前提是一颗完全二叉树，关于完全二叉树，我翻了数据结构一书，描述如下： ad5357f7db1b6a441f589a5062120d41

各版本可能略有不同，但是描述的内容是一样的，即如果用1-n对树从左至右排序的话，我画了一张图帮助理解什么是满二叉树、完全二叉树和非完全二叉树：

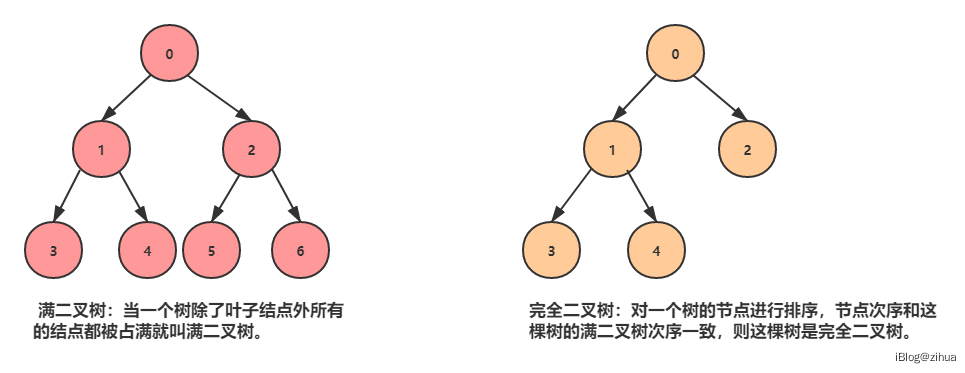
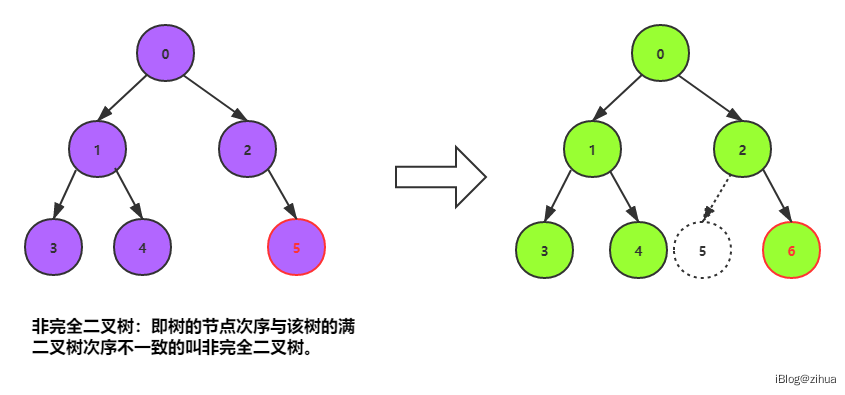
image.png

image.png

完全二叉树（wiki百科）：在一颗二叉树中，除最后一层外，若其余层都是满的，并且最后一层或者是满的，或者是在右边缺少若干个连续节点，则此树为完全二叉树（Complete Binary Tree）。

我们可以知道，如上图，对满二叉树进行自上而下、自左而右的遍历按照下标编号进行读取，则下标依次是0,1,2,3,4,5,6，当我想访问2号元素的父节点、左孩子和右孩子时，可以计算出父节点为(i-1)/2=0，左孩子编号为i×2+1=6，右孩子编号为i×2+2=7。

而完全二叉树也具有满二叉树的这种性质，其最重要的特点就是这样。如果有n个节点的完全二叉树按层序遍历从左往右的顺序从0编号，对于每个节点均可以计算出该节点的父节点、左孩子、右孩子。这个性质可以使二叉树很方便的直接存入数组中，而不用存放于BinaryTree结构中，省下了空间不说，数组还具有程序局部性原理，效率还很高。

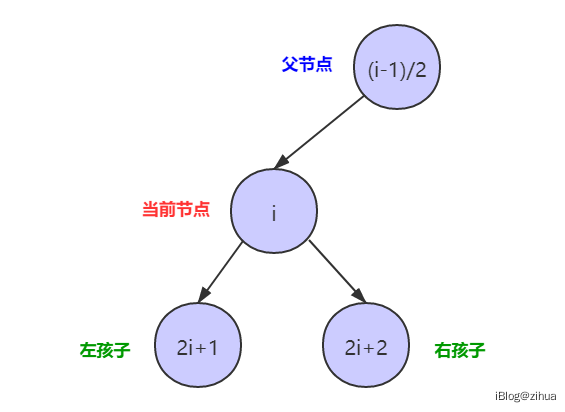
image.png

说了这么多的二叉树，再回过头来了解一下堆，由于堆的前提是一个完全二叉树，所以堆可以直接用数组的形式来表示。

堆还具有这样一个特征，即最小堆和最大堆的特点，堆中任意的节点i，其左右节点均小于等于i节点元素或大于等于i节点元素，如果小于等于，则为最大堆；如果大于等于，则为最小堆。简单的说，对于堆中任意节点元素i，i一定是2i+1和2i+2三个元素中最小或者最大的那一个。映射到数组中则有如下定义：

大顶堆：arr[i] >= arr[2i+1] && arr[i] >= arr[2i+2]

小顶堆：arr[i] <= arr[2i+1] && arr[i] <= arr[2i+2]

堆的实现

当一个堆能够正常构造时，堆顶即为整个数列中最大或者最小的那一个，如何证明堆顶是最大或最小？如下：

1-min (1)

如果我们能建立一个堆，然后记录堆顶，再对除堆顶外的所有元素重新建堆，直至堆的大小为，将所有输出的堆顶串起来的序列，一定是个顺序序列。

堆的常用方法

操作描述时间复杂度
build创建一个空堆O(n)
insert向堆中插入一个新元素O(log n)
update将新元素提升使其符合堆的性质
get获取当前堆顶元素的值O(1)
delete删除堆顶元素O(log n)
heapify使删除堆顶元素的堆再次成为堆

某些特殊的堆的实现还支持其他的一些操作，比如斐波那契堆支持检查一个堆中是否存在某个元素。

堆排序可视化过程

image.png

这个可视化虽然不太直观，但也可以看出，每次都是先找到拿最大的元素，然后放到后面，再对剩下元素重新重复堆排序操作直至所有元素拿完。

堆排序

分3步：

  1. 建立最大堆
  2. 交换堆顶和最堆低元素，堆长度减1
  3. 从现在的堆顶开始重新堆化，重复第2步直至堆长度为1

代码如下：

/**
 *	堆化操作：调整任意节点为堆 
 *	1. 确定最大节点，根?左?右?
 *	2. 交换最大节点与根节点元素
 *	3. 如果根被交换了，说明节点被调整了，所以从被调整的节点开始继续从1开始重复
 */
public void heapify(int pos) {
	int lpos = (pos << 1) + 1;
	int rpos = lpos + 1;
	int max = pos;
	if (rpos >= len) {
		if (lpos < len && heap[lpos] > heap[pos]) max = lpos;
	} else {
		if (heap[lpos] > heap[pos]) {
			max = lpos;
			if (heap[rpos] > heap[lpos]) max = rpos;
		} else {
			if (heap[rpos] > heap[pos]) max = rpos;
		}
	}
	if (max != pos) {
		swap(max, pos);
		heapify(max);
	}
}

/**
 * 	原地堆排序操作：
 * 	1. 先从最后一个非终端节点开始从后往前建立最大堆
 * 	2. 交换最大的堆顶和最后一个元素，并且堆长度减1
 * 	3. 从根开始重新建堆直至堆长度为0
 */
public void sort(int[] arr) {
	set(arr);
	// 1. 建立最大堆
	int index = (heap.length >> 1) - 1;
	for (int i = index; i >= 0; i--) {
		heapify(i);
	}
	// 2. 堆调整
	for (int i = 1; i <= heap.length; i++) {
		if (0 != --len) swap(0, len);
		heapify(0);
	}
}

public static void main(String[] args) {
	int[] arr = RandomData.create(10).random().toArray();
	System.out.println("待排序数量:" + arr.length + "(个)");
	HeapSort proxy = Proxy.proxy(new HeapSort(), RadixSortAspect.class);
	proxy.sort(arr);
}

输出结果：

image.png

时间效率分析

在完成一个堆的建立后，任意局部子堆必然满足堆的定义。但发生交换，比如堆顶和堆最后一个元素交换后，堆的特性消失了，这个时候需要从根开始递归重新建立堆，如果递归的节点发生过交换，说明它的子节点均有可能不满足堆的定义，所以继续递归，从根节点开始最坏的情况下，需要交换[logn]次；在我们拿出堆顶元素后，对继续从根节点开始交换，最坏情况下需要交换[log(n-1)]；如果堆剩下2个元素，最多需要交换[log(2)]次。

由于我们第一次建立大堆顶然后交换堆顶和堆低元素，所以剩余的时间复杂度计算是从n-1~1，假设比较和交换的次数为C(1)，所以，每次堆调整的次数为：

C(n) = C(1)×[log(n-1) + log(n-2) + log(n-3) + ... + log(2)] ≈ C(1) × logn ≈ logn

所以堆调整的时间效率为O(logn)，需要执行n次堆调整直到输出所有最大堆，所以堆排序的效率为O(nlogn)。

空间效率分析

由于我们使用的是原地堆排序，即直接将最大的元素放至最后然后将堆长度减1，不需要开辟额外的空间，空间复杂度为O(1)；如果不用原地的方式那么堆排序需要一个存放有序序列的数组，空间复杂度应为O(n)。

数据统计

从10000开始。

待排序数量:10000(个)
调用sort前系统内存:7.15MB/123.00MB
调用sort前内存使用率:0.06%
调用sort后系统内存:19.50MB/123.00MB
调用sort后内存使用率:0.16%
调用sort所消耗的时间:40毫秒

待排序数量:100000(个)
调用sort前系统内存:10.82MB/123.00MB
调用sort前内存使用率:0.09%
调用sort后系统内存:28.87MB/155.50MB
调用sort后内存使用率:0.19%
调用sort所消耗的时间:139毫秒

待排序数量:1000000(个)
调用sort前系统内存:32.30MB/123.00MB
调用sort前内存使用率:0.26%
调用sort后系统内存:361.38MB/626.00MB
调用sort后内存使用率:0.58%
调用sort所消耗的时间:1450毫秒

待排序数量:10000000(个)
调用sort前系统内存:273.25MB/550.00MB
调用sort前内存使用率:0.50%
调用sort后系统内存:618.34MB/1006.00MB
调用sort后内存使用率:0.61%
调用sort所消耗的时间:18178毫秒

待排序数量:20000000(个)
调用sort前系统内存:639.86MB/806.50MB
调用sort前内存占用:79.34%
调用sort后系统内存:90.96MB/612.50MB
调用sort后内存占用：14.85%
调用sort所消耗的时间:35610毫秒

待排序数量:30000000(个)
调用sort前系统内存:912.01MB/1317.00MB
调用sort前内存占用:69.25%
调用sort后系统内存:321.57MB/831.00MB
调用sort后内存占用：38.70%
调用sort所消耗的时间:59673毫秒

待排序数量:40000000(个)
调用sort前系统内存:1272.71MB/1483.00MB
调用sort前内存占用:85.82%
调用sort后系统内存:241.25MB/862.50MB
调用sort后内存占用：27.97%
调用sort所消耗的时间:91515毫秒

待排序数量:50000000(个)
调用sort前系统内存:1468.56MB/1808.00MB
调用sort前内存占用:81.23%
调用sort后系统内存:481.68MB/1058.50MB
调用sort后内存占用：45.51%
调用sort所消耗的时间:117772毫秒

数据分析

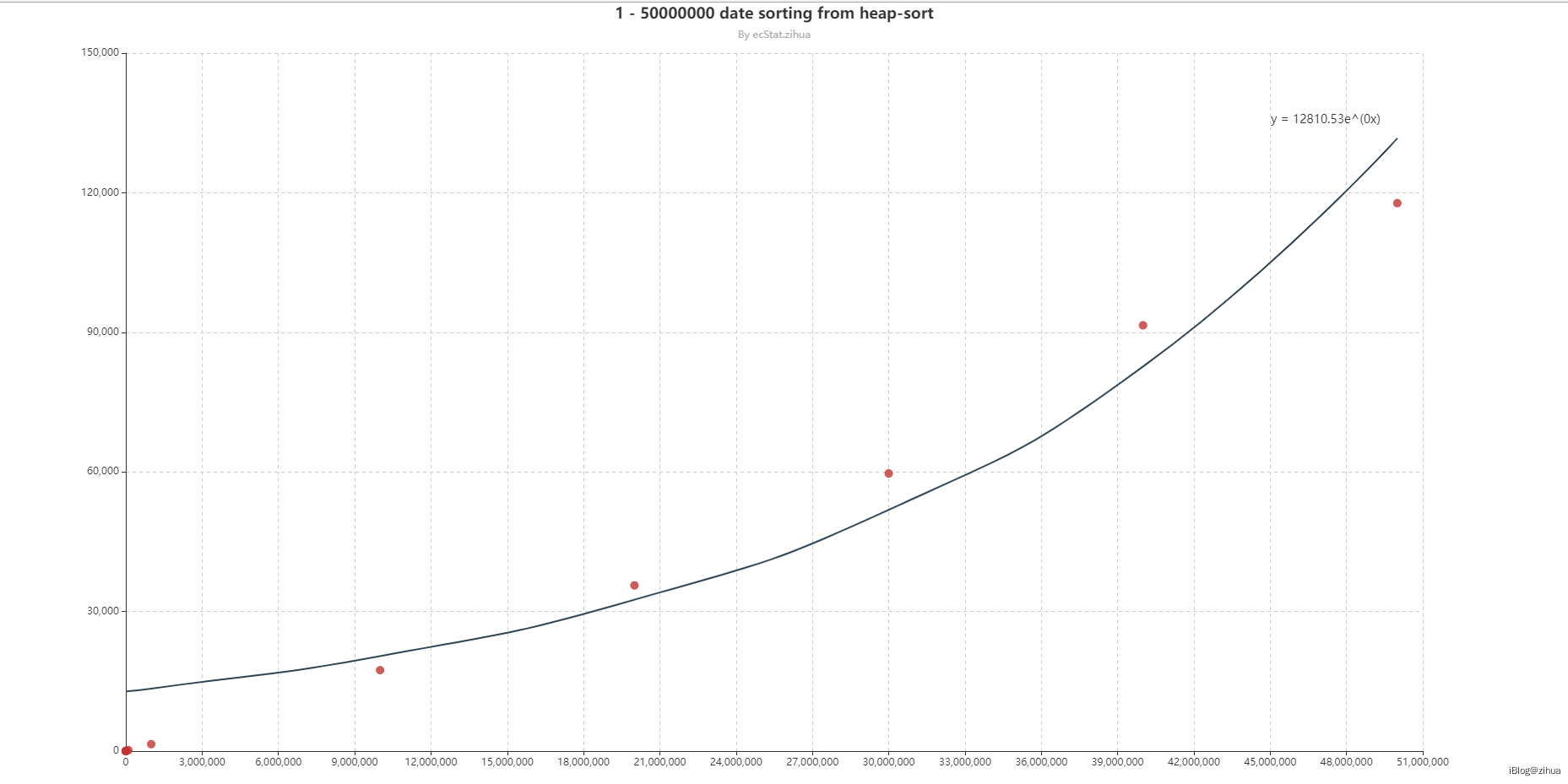
将数据绘制到echarts中： image.png

基本上是以对数的方向增长。

@子华 wechat
欢迎友联！
Donate comment here.